توصيف داده ها با شاخص های آمار

توصيف داده ها با شاخص های آمار-موسسه چشم انداز-آموزش کاربردی GIS و RS

مقدمه

توصیف داده ­ها به کمک شاخص­ های آماری به دو روش غیر مکانی و مکانی انجام می ­شود. در روش غیر مکانی داده ­های جغرافیایی همانند داده های معمولی و بدون در نظر گرفتن وابستگی آنها با مکان توصیف می ­شوند. شاخص ­های آمار توصیفی به دو دسته شاخص­ های مرکزی و پراکندگی تقسیم می ­شوند. سنجه­ هاي گرایش مرکزی (مانند میانه و میانگین و …) و پراکندگی (مانند انحراف­ معیار و واریانس و …)، یک مجموعه داده را به طور خلاصه به صورت عددی نشان می ­دهند (کالت، 1370). سنجش توصیفی داده ­ها ، در ارزیابی مفاهیم بنیادین جغرافیایی مانند سطوح دسترسی و پراکندگی حائز اهمیت می ­باشد. در این فصل مباحث مربوط به توصیف داده ­های جغرافیایی به روش آماری (غیر مکانی) و مکانی مطرح خواهد شد.

الف) توصیف داده­ ها با مهم ترین شاخص­ هاي آماری (غیر مکانی)

نکته مهم در مطالعه توزیع یک نمونه از مقادير، تعیین يک مقدار مرکزی، یعنی مقدار نماینده ­اي که اندازه ­ها در اطراف آن توزیع شده­ اند، به عنوان نقطه تعادل داده ­ها مي­ باشد. از معروفترین شاخص ­های مرکزی مي ­توان به موارد زیر اشاره کرد.

ميانگين حسابي

میانگین حسابی به طور ساده عبارت ست از مجموع تمام مقادير تقسیم بر تعداد آن­ ها. در مورد نمونه­ هاي آماري، ميانگين حسابي از رابطه زير محاسبه مي­ شود:

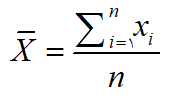
که در آن Xi مقادير خام،

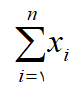
مجموع تمام مقادير و n برای نشان دادن حجم نمونه است. میانگین جامعه (μ) را نيز مي­توان با رابطه ­اي مشابه رابطه فوق محاسبه نمود (پارسیان، 1384). به عنوان مثال مقدار تعادل بارش در يک استان را مي ­توان در آمار کلاسیک با استفاده از ميانگين حسابي محاسبه کرد.

در داده­ هایی که به صورت جدول فراوانی خلاصه شده ­اند و دارای کران پایین و بالای طبقات هستند باید مراحل زیر را برای محاسبۀ میانگین انجام داد.

– باید نقطۀ میان هر طبقه (mi) را بدست آورد.

– متوسط هر طبقه (mi) در مقدار فراوانی مشاهده شده (fi) ضرب می­ شود.

– مشابه میانگین حسابی مراحل کار ادامه پیدا می ­کند. بنابراین

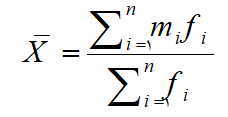
برای درک بهتر به پرسش زیر نگاه کنید.

پرسش 1)

با توجه به مقادير ارائه شده در جدول زیر مقدار میانگین رطوبت نسبی در شیراز را محاسبه کنيد.

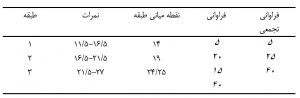
جواب:

به طور متوسط رطوبت نسبی در شهر شیراز برابر با 20/34 می­باشد.

میانگین وزنی

در مواردي که ارزش يا اهميت همه مقادير در محاسبه ميانگين يکسان نيست از ميانگين ­گيري وزني استفاده مي­ شود. به عنوان مثال میزان بارش در مناطق مختلف تحت تأثیر مساحت آن مناطق است و جهت محاسبه ميانگـين بارش کل منـطقه لازم است ميـانگين­ گيـري وزني انـجام داد. براي محاسبه ميانگين وزني از رابطه زير استفاده مي­ شود:

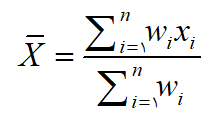
در رابطه فوق xi مقدار و wi عامل وزن هر مقدار مي­ باشد.

پرسش 1)

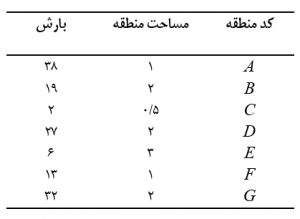
با توجه به مقادير ارائه شده در جدول زیر که نشان دهنده مقدار بارش و مساحت تحت پوشش هر ايستگاه هواشناسي مي ­باشد،به سوالات زیر پاسخ دهید؟

الف) مقدار ميانگين حسابي بارش در منطقه مورد مطالعه را محاسبه کنيد.

ب) مقدار میانگین وزنی بارش را با توجه به مساحت منطقه محاسبه کنید.

جواب:

الف) ميانگين حسابي مقادير بارش برابر با 57/19 ميلي­متر مي ­باشد:

ب) ميانگين وزنی نيز برابر با 54/20 ميلي­متر:

میانگین متحرک

میانگین حسابی به این صورت تعریف شد که اگر یک سری داده داشته باشیم همگی داده­ ها را با هم جمع کرده و سپس جواب به دست آمده را به تعداد کل داده­ ها تقسیم نموده. در اینجا قصد است روشی به نام میانگین متحرک را مطرح کرده که بیشتر در سری زمانی کاربرد دارد. این روش دقیقاً مشابه به دست آوردن میانگین حسابی است اما با این تفاوت که برای یک سری داده چندین بار از میانگین ­گیری استفاده می ­شود. برای نمونه، برای سری داده ­های زیر روش میانگین متحرک مرتبه N به طریق زیر به دست می­ آید:

چون میانگین متحرک مرتبه N است بنابراین در گام اول باید از N تا مشاهده اول میانگین ­گیری شود که با Y1 نشان داده شده است.

در گام دوم داده نخست را کنار گذاشته و باز فرآیند میانگین­ گیری را بر روی N مشاهده انجام می ­شود. که با Y2 نشان داده شده است.

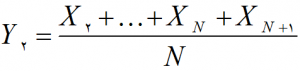
در گام سوم داده نخست مرحلۀ قبل را کنار گذاشته و باز فرآیند میانگین ­گیری را بر روی N تا مشاهده ادامه داده بنابراین Y3 به صورت زیر تعریف می­ شود.

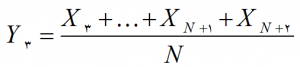
به همین طریق مراحل ادامه پیدا می­ کند.

در مورد محاسبۀ میانگین متحرک با مرتبه N دو حالت اتفاق می ­افتد.

– عدد N فرد است. به عنوان مثال اگر N = 5 باشد اولین مقدار میانگین متحرک در مقابل مشاهده سوم قرار می­ گیرد. به این دلیل که تعریف شد، میانگین نقطه تعادل داده ­است از بین 5 تا داده، مشاهده سوم هر سری که میانگین متحرک آن محاسبه می­ شود معرف نقطه تعادل داده است.

– عدد N زوج است. در این حالت مقادیر محاسبه شده میانگین ­های متحرک دقیقاً در مقابل مشاهدات سری زمانی قرار نمی­ گیرند بلکه بین دو مشاهده متوالی واقع می ­شوند در این مورد با در نظر گرفتن متوسط دو میانگین متحرک و قرار دادن آن در مقابل مشاهده متناظر، آن­ها را با داده های اولیه همزمان می­ کنند. برای نمونه، اگر N = 4 باشد اولین میانگین متحرک بین مشاهده دوم و سوم قرار می­ گیرد و دومین میانگین متحرک بین مشاهدات سوم و چهارم واقع می­ شود به همین ترتیب الی آخر.

پرسش 1)

با توجه به مقادير ارائه شده زیر به سوالات زیر پاسخ دهید.

الف) میانگین متحرک مرتبه 3 را مشخص کنید.

ب) با وزن­های 1,4,1 میانگین متحرک وزنی مرتبۀ 3 را مشخص کنید.

2,6,1,5,3,7,2

جواب:

الف)

مرحلۀ 1)

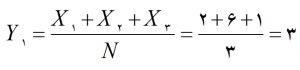
مرحلۀ 2)

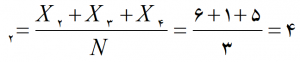
و …

پاسخ­ها باید به ترتیب برابر با 4,5,3,4,3 به دست آید.

ب) با توجه به این که W =W1+W2+W3

این مراحل به همین صورت ادامه پیدا می­کند.

ميانه

ميانه مقداری است که دسته­ داده ­ها را به دو قسمت مساوی تقسیم می­ کند. به عبارت دیگر 50 درصد داده­ ها در زیر میانه و 50 درصد در بالای میانه قرار می­ گیرند. برای پیدا کردن میانه در داده­ های گسسته، ابتدا داده­ ها از کوچک به بزرگ مرتب مي­ شوند. در اين حالت اگر تعداد داده­ ها فرد باشد، عدد وسط، میانه است و اگر تعداد داده­ ها زوج باشد میانه برابر با میانگین حسابی دو عدد وسطی است. برای نمونه، ميانه داده­ هاي زير برابر با 22 است چون داده­ ها ترتيب صعودي داشته و عدد وسط برابر با 22 است:

23،22،22،21،20

اما در مورد داده ­هاي زير مقدار ميانه برابر با 16/5 است چون در يک ترتيب صعودي، تعداد اعداد زوج است، ميانگين دو عدد وسط يعني 16/5=2/(15+16) برابر با مقدار ميانه است:

12،14،15،16،16،17

میانه اعداد همواره وجود دارد. حجم اعداد بزرگ در مقدار میانه تأثیری ندارد. به عبارتی دیگر میانه نسبت به اعداد بزرگ یا کوچک حساس نیست. بنابراین در مواقعی که مقادير افراطی خیلی بزرگ و یا خیلی کوچک در میان داده­ ها وجود داشته باشد، میانه بهترین شاخص مرکزی است.

مد (نما)

عبارت ست از عددی که بیشترین فراوانی را دارد یا بیشتر از دیگران تکرار شده باشد. در بین اندازه ­های گرایش به مرکز تنها نما را می ­توان برای داده ­ها با مقیاس اسمی (کیفی) به کار برد.

مد (نما) ممکن است وجود نداشته باشد یا این که بیشتر از یکی نیز باشد. و تحت تأثیر بزرگترین و کوچکترین داده نیز قرار نمی ­گیرد.

شاخص­ هاي پراکندگي

شاخص ­هاي مرکزي تمایل داده ­ها به نقطه مرکزي را به خوبي نشان مي­ دهند اما قادر به ارائه اطلاعات کافی از تغییر پذیری، تنوع و چگونگی توزیع مقادیر در اطراف اين نقطه نمي ­باشند. بنابراين در بيشتر موارد آماره ­هاي مزبور جواب گوی نیاز پژوهشگر به شناخت واقعیت­ های طبیعی نيستند و لازم است مشاهدات براساس شدت نوسان حول یک نقطه مرکزي مورد بررسی و مقایسه قرار گیرد. در نهايت اين­که بررسي آماره ­هاي پراکندگی در کنار آماره­ هاي مرکزی اطلاعات مناسبی از مجموعه داده­ های آماري را در اختيار قرار مي ­دهد.

در مقايسه شاخص­ هاي مرکزي و پراکندگي مي­ توان برای نمونه دمای دو ایستگاه فرضی الف و ب طی 6 ماه سال را به صورت زیر در نظر گرفت:

میانگین حسابي دماي در هر دو ایستگاه برابر با 3/7 درجه می­ باشد. در ایستگاه الف تغییرات دما حول میانگین کم است اما در ايستگاه ب تغییرات زیادی نسبت به میانگین ديده مي­ شود. دما در اين ایستگاه در برخی ماه ­ها فاصله زیادی از میانگین دارد و پر افت و خیزتر از ایستگاه الف است. به طور ساده برای محاسبه پراکندگی، اختلاف دما نسبت به میانگین (نقطه تعادل داده­ ها) محاسبه مي­ شود:

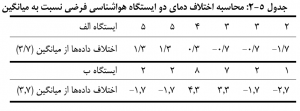
در جدول فوق اختلافات به صورت مثبت و منفی نشان داده شده است. از آنجايي كه جمع جبري انحرافات اعضا از ميانگين صفر مي­ شود. می­ توان اختلافات را به توان 2 رساند و آن­ها را با علامت مثبت نشان داد:

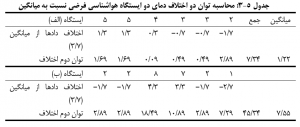
جدول بالا نشان مي­ دهد که به طور متوسط مجموع توان دوم اختلاف برای ایستگاه (الف) برابر با 1/22 و برای ایستگاه (ب) برابر با 7/55 است که بیانگر پراکندگی بیشتر در ایستگاه (ب) می ­باشد. فرآیند ساده­ اي که در مثال بالا انجام شد معرف آماره واریانس است. همچنین می­ توان چون جمع جبری انحرافات از میانگین برابر صفر است از قدر مطلق از قدر مطلق اين فاصله ها استفاده شود. متوسط قدر مطلق اين انحرافات يا فاصله ها انحراف متوسط ناميده مي­ شود.

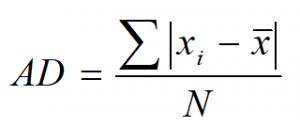
كه در آن، AD، انحراف متوسط است.

واریانس جامعه

واريانس جامعه یکی از مهمترین شاخص­ های پراکندگی است که در بخش قبل راجع به محاسبۀ آن توضیح داده شد. این شاخص با رابطه زير محاسبه مي­ شود:

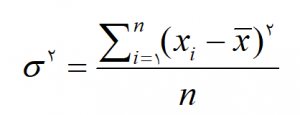
واریانس نمونه با S2 يا Var نشان داده می­ شود.

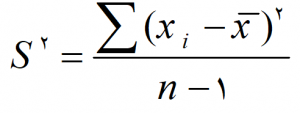
چون در محاسبه واریانس از توان دوم اختلافات استفاده مي ­شود بنابراین واحد در واریانس به صورت توان دوم واحد داده ­هاست. لازم به ذکر است که هر قدر فاصله عضوي از ميانگين كمتر باشد به مركز يا ميانگين داده ­ها نزديكتر باشد جمعيت از تراكم يا تجانس بالاتری برخوردار است.

انحراف معيار جامعه

انحراف معيار، مهمترین و کارآمدترین آماره پراکندگي است و براي جامعه از رابطه زير به دست مي­ آيد:

گاهی اوقات مخرج رابطه فوق n می­ باشد اما استفاده از n-1 برآورد بهتری از انحراف معیار جامعه به دست مي ­دهد. انحراف معيار نمونه با S يا SD نشان داده مي­ شود.

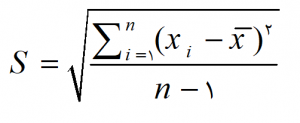
انحراف معيار به جهت همخواني با واحد داده ها كاربرد بسياري دارد. هرقدر اندازه انحراف معيار بيشتر شود ميزان تفرق و پراكندگي داده ها بيشتر است.

دامنه­ ی میان چارکی

برابر با اختلاف چارک سوم از چارک اول تعریف می ­شود. وجود مشاهده خیلی بزرگ یا خیلی کوچک در این معیار اثری نمی­ گذارد.

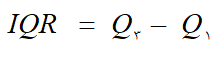
دامنه تعييرات

ساده ترين شاخص اندازه گيري پراكنش داده ­ها است که عبارت است از تفاوت بين بالاترين و پائين ترين ارزش داده ها.

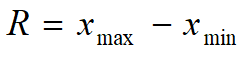
شاخص پراکندگی چارکی

با توجه به اينكه شاخص دامنۀ بین چارکی ارزش­ هاي بالاترين و پائين ترين را در بر نمي­ گيرد از ثبات بيشتري برخوردار است. بدین جهت از اين شاخص براي مقايسه تمركز اعضا در ارزش­ هاي بالاتر يا پائين تر از ميانه استفاده مي­ شود:

كه در آن Yyk، شاخص يول كندال است. در صورت مثبت بودن Yyk اعضاي بالاتر از ميانه در فاصله بيشتري از ارزش­ ها پخش شده­ اند ولي اعضاي پائين تر از ميانه در فاصله کوتاه تری متمركز شده ­اند و توزيع اعضاي سري داده­ ها كشيدگي مثبت دارد. به عبارت دیگر تراکم نسبی اعضای کم فراوان تر است. شاخص Yyk منفي بيانگر كشيدگي منفي داده ­ها است. يعني تراكم داده­ ها در چارك بالاتر از ميانه بيشتر از چارك پائين تر از ميانه است.

ضريب تغيير پذيري

ضریب تغییر پذیری شاخص استانداردی برای بیان میزان پراکندگی یک سری آماری و مقایسه میزان پراکندگی چند سری آماری به کار می ­رود. این شاخص از مقیاس داده ­ها مستقل است و به صورت درصد بیان می­ شود و از رابطه زیر محاسبه می شود:

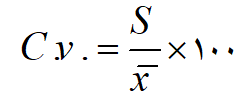
كه در آن C.v ضريب تغيير پذيري به درصد؛ S، انحراف معيار؛ و

ميانگين سري آماري است. هرقدر انحراف معيار در مقابل ميانگين كوچك تر باشد بيانگر اين است كه همه داده­ ها در فاصله كمتري از ميانگين متمركز شده­ اند و جمعيت آماري از تجانس بالايي برخوردار است. در اين صورت مقدار C.v هم بسیار کمتر خواهد شد و مقدار میانگین از ثبات بیشتری برخوردار است.