داده کاوی مکانی - فضایی :کشف الگوهای پنهان در عوارض - هوش پیروزی

سیستم اطلاعات جغرافیایی (GIS)و پایش مخاطرات زیست‌محیطی تحت تغییرات آب و هوا: بررسی گسترده

مقدمه ای بر داده کاوی فضایی

هدف داده کاوی مکانی کشف الگوهای بالقوه مفید، جالب و غیر پیش پا افتاده از مجموعه داده های مکانی است (به عنوان مثال، مسیر GPS گوشی های هوشمند). داده کاوی مکانی از نظر اجتماعی دارای کاربردهایی در بهداشت عمومی، ایمنی عمومی، علوم آب و هوا و غیره است. به عنوان مثال، در اپیدمیولوژی، داده کاوی مکانی به یافتن مناطقی با غلظت بالای حوادث بیماری برای مدیریت شیوع بیماری کمک می کند. روش‌های محاسباتی برای کشف الگوهای فضایی مورد نیاز است زیرا حجم و سرعت داده‌های مکانی بیش از توانایی متخصصان انسانی برای تجزیه و تحلیل آن است. داده‌های مکانی دارای ویژگی‌های منحصربه‌فردی مانند خودهمبستگی مکانی و ناهمگنی فضایی هستند که فرض iid (مستقل و توزیع‌شده مشابه) روش‌های آماری سنتی و داده‌کاوی را نقض می‌کنند. از این رو، استفاده از روش‌های سنتی ممکن است الگوها را از دست بدهد یا الگوهای جعلی را به همراه داشته باشد که در کاربردهای اجتماعی پرهزینه هستند. علاوه بر این، چالش‌های دیگری مانند MAUP (مشکل واحد منطقه‌ای قابل تغییر) وجود دارد، همانطور که در یک پرونده دادگاه اخیر در مورد بحث در مورد جعلی در انتخابات نشان داده شده است. در این مقاله، ابزارها و روش‌های محاسباتی داده‌کاوی مکانی را با تمرکز بر خانواده‌های الگوی فضایی اولیه مورد بحث قرار می‌دهیم: تشخیص نقطه‌های مهم، تشخیص هم‌مکانی، پیش‌بینی فضایی، و تشخیص نقاط پرت فضایی. روش‌های تشخیص Hotspot از اطلاعات دامنه برای مدل‌سازی دقیق مناطق فعال‌تر و با تراکم بالا استفاده می‌کنند. روش‌های تشخیص هم‌سویی اشیایی را پیدا می‌کنند که نمونه‌های آن‌ها در مجاورت یکدیگر در یک مکان هستند. رویکردهای پیش‌بینی فضایی به صراحت رابطه همسایگی مکان‌ها را برای پیش‌بینی متغیرهای هدف از ویژگی‌های ورودی مدل‌سازی می‌کنند. در نهایت، روش‌های تشخیص پرت فضایی داده‌هایی را پیدا می‌کنند که با همسایگانشان متفاوت است. در نهایت، ما تحقیقات و روندهای آینده در داده کاوی مکانی را توصیف می کنیم.

توضیحات موضوع:

تعاریف
معرفی
آمار فضایی
خانواده های الگوی فضایی
بحث و رهنمودهای آینده

1. تعاریف

داده های مکانی : هر داده ای که شامل اطلاعات مکان مانند آدرس خیابان، یا طول و عرض جغرافیایی باشد.

فرض مستقل و توزیع شده یکسان (iid) : یک فرض کلاسیک در آمار است که فرض می کند نمونه های داده مستقل از یکدیگر هستند و به طور یکسان توزیع می شوند.

خودهمبستگی فضایی : به عنوان معیاری از وابستگی بین نقاط در یک همسایگی فضایی تعریف می شود. وابستگی داده های مکانی فرض استقلال آمار کلاسیک را رد می کند.

ناهمگونی فضایی (یا غیر ایستایی فضایی) : به تنوع در رویدادها، ویژگی ها و روابط در یک منطقه اشاره دارد. این فرض توزیع یکسان را نقض می کند.

پیوستگی فضایی y: به وجود وابستگی فضایی یا همبستگی فضایی در داده های ورودی در فضا اشاره دارد.

آمار فضایی : تعمیم آمارهای سنتی برای داده‌های مکانی که مدل‌سازی وابستگی و ناهمگونی مکانی را ممکن می‌سازد.

داده کاوی فضایی : تعمیم داده کاوی سنتی که به بررسی مبادلات بین مقیاس پذیری محاسباتی و دقت ریاضی برای داده های مکانی می پردازد.

2. مقدمه

رشد قابل توجه داده های آگاه از مکان (به عنوان مثال، ردیابی GPS تلفن های هوشمند، تصاویر ماهواره ای سنجش از راه دور) و پیشرفت های اخیر در زیرساخت های رایانه ای نیاز به سیستم های خودکار برای کشف الگوهای فضایی در داده ها را برجسته می کند. داده کاوی مکانی (SDM) فرآیند کشف الگوهای غیر پیش پا افتاده، جالب و قبلاً ناشناخته، اما بالقوه مفید از پایگاه داده های بزرگ مکانی و مکانی-زمانی است (Han and Miller 2009, Shekhar et al. 2015b; Xie et al. 2017; شکر و ولد 2020). با توجه به مجموعه داده های جغرافیایی، سه مرحله کلیدی برای تشخیص الگوهای مکانی به شرح زیر است: 1) پیش پردازش داده ها برای تصحیح نویز، خطا، و اطلاعات از دست رفته همراه با تجزیه و تحلیل فضا-زمان برای شناسایی توزیع فضایی یا مکانی-زمانی زمینه، 2) اعمال یک الگوریتم SDM مربوط به داده های از پیش پردازش شده برای تولید یک الگوی خروجی، 3) پس از پردازش الگوی خروجی، و سپس 4) داشتن کارشناسان حوزه تجزیه و تحلیل خروجی برای شناسایی بینش های جدید. اصلاح بیشتر الگوریتم SDM ممکن است بر اساس تفسیر نتایج در آخرین مرحله مورد نیاز باشد.

تکنیک‌های SDM برای سازمان‌های بزرگی که بر اساس مجموعه‌های بزرگ داده‌های مکانی تصمیم‌گیری می‌کنند و خط‌مشی‌ها را اتخاذ می‌کنند، حیاتی هستند. جدول 1 برخی از دامنه ها و برنامه های کاربردی SDM مربوطه را فهرست می کند. به عنوان مثال در محیط زیست و مدیریت زیست محیطی، دانشمندان تصاویر سنجش از دور را به طبقات (به عنوان مثال، پوشش گیاهی، تالاب، و غیره) بر روی نقشه پوشش زمین طبقه بندی می کنند. در امنیت عمومی، کشف رویدادهای نقاط جرم و جنایت ممکن است به ادارات پلیس در تخصیص مؤثر منابع کمک کند. همچنین، در علم آب و هوا، یافتن اثرات مکان های دور بر دمای یک مکان معین می تواند به تخمین دما دقیق تری منجر شود.

**جدول 1: نمونه هایی از حوزه های کاربردی داده کاوی مکانی**
دامنه	نرم افزار داده کاوی فضایی
امنیت عمومی	کشف الگوهای نقاط داغ از نقشه های رویداد جنایی
همهگیرشناسی	تشخیص شیوع بیماری
کسب و کار	تخصیص بازار برای به حداکثر رساندن سود فروشگاه ها
علوم اعصاب	کشف الگوهای فعالیت مغز انسان از تصاویر عصبی
علوم آب و هوا	یافتن همبستگی های مثبت یا منفی بین دمای مکان های دور

ورودی داده های SDM شامل ویژگی های مکانی مانند طول جغرافیایی، طول جغرافیایی و ارتفاع است که برای تعیین موقعیت مکانی و وسعت اشیاء فضایی استفاده می شود. اشیاء فضایی شامل اشیاء توسعه یافته مانند نقاط، خطوط و چندضلعی ها هستند. روابط فضایی بین اشیا منبعی حیاتی و غنی از اطلاعات است که می تواند انتخاب ویژگی را برای بهبود عملکرد روش های سنتی افزایش دهد. علاوه بر این، داده‌کاوی سنتی و تکنیک‌های یادگیری ماشین ممکن است الگوها را از دست بدهند یا ممکن است الگوهای جعلی را به همراه داشته باشند که هزینه بالایی دارند (مثلاً انگ زدن). این به دلیل ماهیت داده های مکانی است (به عنوان مثال، خودهمبستگی مکانی و ناهمگنی فضایی) که فرض کلاسیک در آمار را نقض می کند، یک مشکل رایج در تکنیک های داده کاوی و یادگیری ماشین.

آمار مکانی و داده کاوی مکانی زمینه های همپوشانی هستند که در بسیاری از جنبه ها از یکدیگر پشتیبانی می کنند. آمار فضایی بسیاری از آمارهای آزمایشی را مورد بررسی قرار داده است که می تواند از طراحی رویکردهای داده کاوی مکانی خبر دهد. تکنیک های آماری دارای دقت ریاضی بالایی هستند، با این حال، مقیاس پذیری محاسباتی ملاحظات اولیه نیست. در مقابل، تکنیک های SDM به صراحت به یک مبادله بین دقت ریاضی و مقیاس پذیری محاسباتی برای تجزیه و تحلیل داده های بزرگ فضایی می پردازد. شکل 1 مبادله بین آمار مکانی، داده کاوی و داده کاوی مکانی را نشان می دهد. در بخش 4 به تفصیل بیشتر می پردازیم.

مبادله بین آمار مکانی، داده کاوی مکانی، داده کاوی سنتی

شکل 1. یک مثال گویا از مبادله بین آمار مکانی، داده کاوی مکانی و تکنیک های سنتی داده کاوی. منبع: نویسندگان

محدوده: هدف این مقاله برجسته کردن تفاوت بین داده‌کاوی مکانی، داده‌کاوی سنتی و خانواده‌های الگوی فضایی است. با این حال، ما آمار فضایی و ریاضیات مربوط به آن را به تفصیل مورد بحث قرار نمی دهیم. علاوه بر این، شرح مفصل تکنیک‌های سنتی داده‌کاوی خارج از محدوده این مقاله است که مخاطبان علاقه‌مند می‌توانند به عنوان راهنمای جامع در آن موضوعات به (تان، اشتاین‌باخ و کومار 2016) مراجعه کنند. یکی دیگر از زیر زمینه های کلیدی در داده کاوی فضایی، داده کاوی مسیر است و شرح مفصل تکنیک های داده کاوی مسیری خارج از محدوده این مقاله است. خوانندگان علاقه مند می توانند به ژنگ (2015) مراجعه کنند که یک نظرسنجی جامع در مورد داده کاوی مسیر ارائه می دهد. در نهایت، داده کاوی مکانی به طور گسترده در بسیاری از رشته ها (مانند سنجش از دور، جغرافیا) و حوزه های مرتبط (مانند،
سازمان : مقاله به شرح زیر تنظیم شده است. بخش 2 پیشینه مختصری در مورد آمار مکانی ارائه می دهد. بخش 3 چهار خانواده الگوی مهم، کاربردهای مرتبط با آن و روش های آماری را توضیح می دهد. در بخش 4، نکات برجسته کوتاهی از تفاوت بین آمار مکانی و داده کاوی مکانی و به دنبال آن تحقیقات و روندهای آتی ارائه شده است.

2. آمار فضایی

آمار فضایی (Cressie 2015، Gelfand 2010) به ویژگی‌های فضایی خود همبستگی و ناهمگنی پایبند است. این با آمار سنتی که توزیع مستقل و یکسان (iid) داده های نمونه را برای محاسبات خود فرض می کند، متفاوت است. فرض iid اساس اکثر روش های داده کاوی و قضایای آمار است. این مبنای روش های شناخته شده ای مانند تخمین حداکثر درستنمایی و قضیه حد مرکزی است. وابستگی داده های مکانی یک واقعیت شناخته شده است که به عنوان اولین قانون جغرافیا در نظر گرفته می شود: “همه چیز به هر چیز دیگری مربوط است، اما چیزهای نزدیک بیشتر از چیزهای دور مرتبط هستند”.

آمار فضایی به پارتیشن بندی فضا حساس است و مقادیر به شکل و مقیاس پارتیشن ها بستگی دارد. این مفهوم به طور رسمی به عنوان مسئله واحد منطقه ای قابل اصلاح (MAUP) نامیده می شود. از آن به عنوان اثر چند مقیاسی نیز یاد می شود. به عنوان مثال، نتایج زمانی که در ایالت ها در مقابل سطح خانوار جمع شوند، می توانند متفاوت باشند. احزاب ولسوالی های انتخاباتی نمونه بارز دیگری از MAUP است که در آن احزاب سیاسی مرزهای حوزه ها را دوباره ترسیم می کنند تا امکان پیروزی خود را بهبود بخشند. شکل 2 نمونه ای از جست و خیز را نشان می دهد که در آن جمعیت 15 نفری که از نامزد A حمایت می کنند و جمعیت 10 نفری که از نامزد B حمایت می کنند باید به 5 ناحیه کنگره تقسیم شوند. فقط یک طرح پارتیشن منصفانه است (شکل 2c).

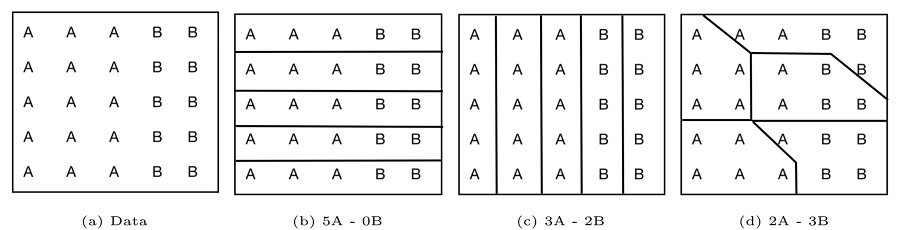
نمونه جست و خیز

شکل 2. نمونه ای از جریماندرینگ. (الف) داده های پایه؛ (ب) پارتیشن بندی افقی، A تمام صندلی ها را می گیرد، 5A – 0B. (ج) پارتیشن بندی عمودی، 3A – 2B. (د) تقسیم بندی برای کمک به اقلیت B برای کسب اکثریت کرسی ها، 2A – 3B. منبع: نویسندگان

مثال زیر نشان می دهد که انتخاب یک مدل فضایی مناسب در SDM بسیار مهم است. در شکل 3a، سه نوع نقطه، مربع $(\مربع)$ ، دایره $(\bigcirc)$ و مثلث $(\مثلث)$ وجود دارد. هر نوع نقطه دارای دو نمونه است. برای محاسبه همبستگی فضایی بین نقاط مختلف، همانطور که در شکل 3b و 3c نشان داده شده است، فضا را تقسیم بندی می کنیم. توزیع فضایی هر نوع نقطه یک بردار ویژگی است که با تعداد آن در هر پارتیشن مطابقت دارد. همانطور که در جدول 2a نشان داده شده است، بر اساس تقسیم بندی منطقه (به عنوان مثال، شکل 3b و شکل 3c)، همبستگی های پیرسون و پشتیبانی بین $(\bigcirc، \مثلث)$ و $(\bigcirc، \square)$ متنوع هستند. همبستگی بین مثلث ها و دایره ها در شکل 3b منفی است، اما همبستگی بین مثلث ها و دایره ها در شکل 3b مثبت است. از سوی دیگر، پارتیشن بندی منطقه در شکل 3c نتایج مخالف را در مقایسه با شکل 3b نشان می دهد. بنابراین، نتایج و روابط فضایی بر اساس نحوه تقسیم‌بندی منطقه مورد مطالعه متفاوت است. همانطور که در شکل 3b و 3c نشان داده شده است، رابطه فضایی بین دایره ها و مثلث ها و دایره ها و مربع ها به دلیل تقسیم بندی های مختلف از بین می رود. در مقابل، شکل 3d نشان می دهد که یک شاخص مشارکت (جدول 2b) قادر است مجاورت را به دقت نشان دهد.

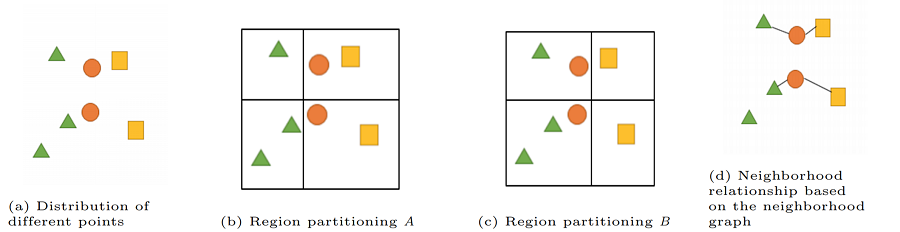
نمونه هایی از آمار فضایی

شکل 3. نمونه هایی از آمار فضایی. منبع: نویسندگان

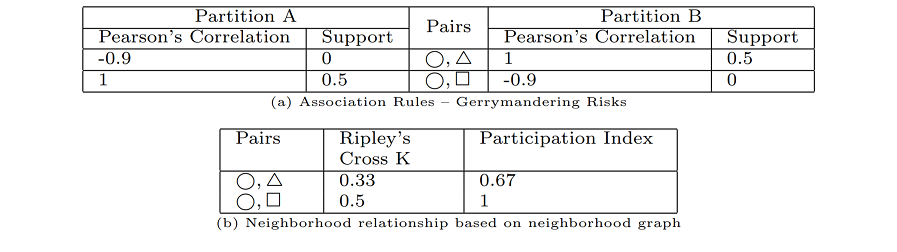
جدول 2. ضریب همبستگی پیرسون برای تقسیم بندی منطقه و شاخص مشارکت برای نمودار همسایگی. نتایج نشان می دهد که پارتیشن بندی روابط فضایی را می شکند، در حالی که نمودار همسایگی رابطه را حفظ می کند.

همبستگی پیرسون و MAUP

روش‌ها در آمار مکانی (Waller and Gotway 2004) را می‌توان بر اساس نوع داده‌های ورودی به صورت زیر دسته‌بندی کرد: 1) زمین آمار برای داده‌های نقطه‌ای مرجع، 2) آمار شبکه برای داده‌های منطقه، و 3) فرآیندهای نقطه‌ای مکانی برای الگوهای نقطه‌ای مکانی.

زمین آمار. زمین آمار تداوم فضایی و ایستایی ضعیف را تجزیه و تحلیل می کند (Cressie 2015)، که ویژگی های ذاتی مجموعه داده های مکانی هستند. تکنیک های زمین آماری بر مدل های آماری متکی هستند که از متغیرهای تصادفی برای مدل سازی عدم قطعیت استفاده می کنند. زمین آمار طیفی از ابزارهای آماری مانند کریجینگ را برای درون یابی مقدار یک میدان تصادفی در مکان های نمونه برداری نشده ارائه می دهد.
آمار شبکه: شبکه مدلی برای تعیین نواحی گسسته در یک توزیع فضایی است. این تعداد محدودی از شبکه ها در یک حوزه فضایی است. یک ماتریس W برای تبدیل داده های پیوسته اصلی به یک نمایش گسسته بر اساس روابط همسایگی فضایی استفاده می شود (شخار و همکاران 2011).
فرآیند نقطه ای: فرآیند نقطه ای روشی آماری برای تولید توزیع نقطه ای است. احتمال قرار گرفتن یک نقطه در یک مکان در منطقه مورد مطالعه را تعیین می کند. یک توزیع پواسون همگن (به عنوان مثال، شکل 4a) احتمال یکسانی در همه مکان ها دارد، که اغلب به عنوان یک فرضیه صفر استفاده می شود. دو فرض دیگر برای ایجاد مکان مجموعه‌ای از نقاط، خوشه‌بندی (شکل 4b) و خوشه‌ای (شکل 4c) هستند.

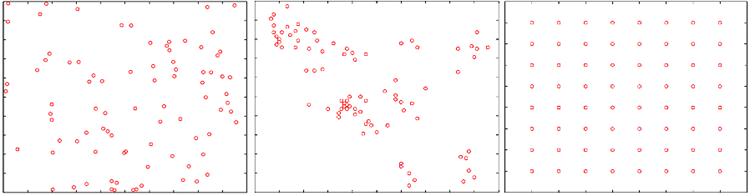
الگوهای نقطه ای تحت فرضیات آماری مختلف

شکل های 4a-4c. مجموعه نمونه هایی از نقاط تحت سه فرض آماری مختلف. چپ/الف: تصادفی فضایی کامل (CSR). مرکز/ب: خوشه ای. راست/ج: خوشه‌زدایی/یکنواخت. منبع: نویسندگان

3. خانواده های الگوی فضایی

روش های داده کاوی مکانی برای تشخیص الگوهای فضایی طراحی شده اند (شخار و همکاران 2011). ما بر روی چهار خانواده الگوی مهم تمرکز می کنیم، یعنی نقاط داغ، همنشینی ها، پیش بینی های فضایی و نقاط پرت فضایی. این خانواده های الگو به طور گسترده در بسیاری از حوزه های مرتبط اجتماعی مانند اپیدمیولوژی، جرم شناسی، ایمنی ترافیک، بوم شناسی، علوم محیطی، علوم آب و هوا، برنامه ریزی شهری و غیره کاربرد دارند.

3.1 تشخیص هات اسپات

با توجه به مجموعه ای از نقاط جغرافیایی که به یک فعالیت در یک حوزه فضایی مربوط می شود، نقاط داغ مناطقی هستند که در مقایسه با سایر مناطق فعال تر و تراکم نقاط بیشتری دارند. کار جان اسنو در سال 1854 یک نمونه اولیه از تشخیص نقاط حساس فضایی بود، جایی که او با موفقیت منبع شیوع وبا را شناسایی کرد. او دریافت که بیشترین میزان بروز بیماری در مجاورت پمپ آب خیابان Broad است (شکل 5a را ببینید). این یک مثال گویا است که اهمیت تشخیص نقاط حساس را در حوزه اپیدمیولوژی نشان می دهد. با این حال، باید توجه داشت که مفهوم یک هات اسپات یک دامنه خاص است و تکنیک های تشخیص هات اسپات باید دانش دامنه را برای مدل سازی صحیح و موثر مناطق هات اسپات در نظر بگیرند. مثلا،

با توجه به کاربردهای گسترده تشخیص هات اسپات، مجموعه‌های نرم‌افزاری برای شناسایی نقاط داغ در مجموعه داده‌های مکانی و مکانی-زمانی توسعه یافته‌اند. SatScan یکی از برجسته ترین نرم افزارهای رایگانی است که برای تشخیص هات اسپات (Kulldorff nd) استفاده می شود. این بر تست فرضیه برای نقاط حساس کاندید است که توسط یک اسکن استوانه ای از فضا کشف می شود. فرضیه صفر بر اساس تصادفی کامل فضایی (CSR) است. فرضیه جایگزین بیان می کند که رویدادها در داخل استوانه تراکم تر از خارج هستند. یک کاندید از نظر آماری معنی دار در نظر گرفته می شود، اگر دارای بالاترین نسبت احتمال ورود به سیستم در بین تمام نقاط حساس نامزد باشد (شکل 5b را ببینید).

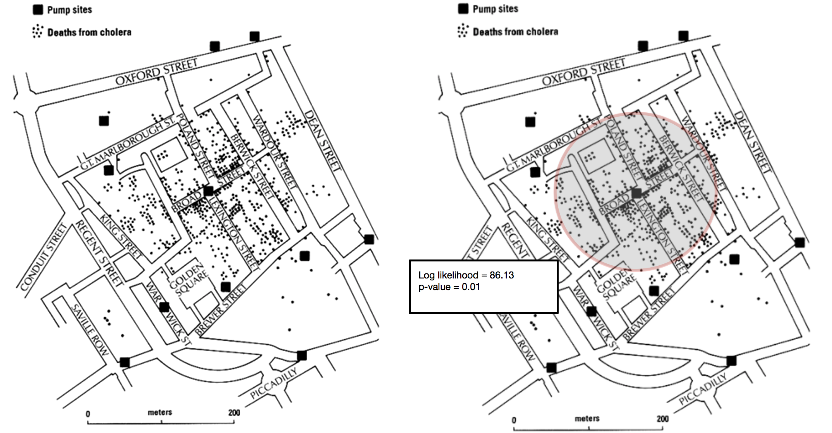
پمپ وبا جان اسنو

شکل 5a-5b. تجزیه و تحلیل محل پمپ آب و مرگ و میر ناشی از وبا در لندن در سال 1854. منبع: نویسندگان.

3.2 تشخیص همسویی

الگوهای ترکیب فضایی (موهان و همکاران 2012) زیرمجموعه هایی از ویژگی هایی را نشان می دهند که نمونه های آنها در نزدیکی یکدیگر قرار دارند. برای مثال، رابطه همزیستی بین تمساح نیل و پرنده سهره مصری الگوی هم‌آمیزی را نشان می‌دهد. بسیاری از وابستگی‌های بیولوژیکی الگوهای هم‌آمیزی را نشان می‌دهند. شکل 6a توزیع فضایی شناسایی شده از طریق الگوریتم ترکیبی از نمونه های پنج ویژگی، یعنی سهره، تمساح، درختان سبز، درختان خشک، و آتش سوزی را نشان می دهد. تجزیه و تحلیل مشابه در مجموعه داده های جرم نشان می دهد که میله ها با دعواهای خیابانی ترکیب می شوند.

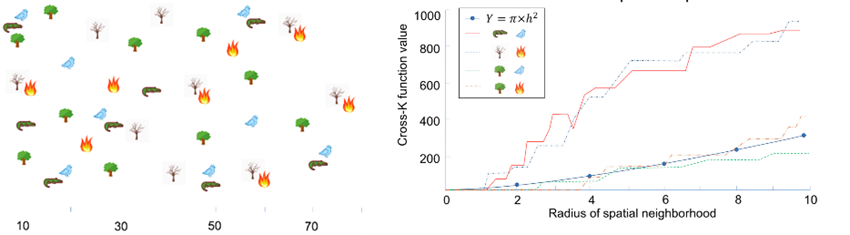
الگوهای کولوکیشن

شکل 6. نمونه ای از تشخیص الگوهای collocation. منبع: نویسندگان

برای اندازه گیری درجه خوشه بندی در یک توزیع نقطه ای، می توانیم از تابع K ریپلی (بخش 4) استفاده کنیم. بر اساس میانگین تعداد نقاطی است که فاصله آنها از یک آستانه از پیش تعریف شده از هر نقطه انتخابی کمتر است. فرضیه صفر K ریپلی نیز بر CSR متکی است. تابع cross-K تابع K ریپلی را به مواردی که چندین ویژگی وجود دارد گسترش می دهد. این یک روش آماری فضایی برای تشخیص الگوهای هم‌آمیزی بین ویژگی‌های رویدادهای نقطه‌ای است. تابع متقاطع K(h) برای ویژگی های فضایی باینری به صورت زیر تعریف می شود:

$K_{ij}(h) = \lambda_j^{-1}\textsf{E\kern-1exE}$ [تعداد j نمونه ها در فاصله h از یک نمونه I که به طور تصادفی انتخاب شده است]، (1)

که $\lambda_j$ در آن چگالی (تعداد در واحد سطح) نمونه های نوع j و h فاصله است. شکل 6b نتایج تابع متقاطع K را برای ورودی نشان داده شده در شکل 6a نشان می دهد. همانطور که مشاهده می شود، کروکودیل و سهره دارای مقادیر متقاطع K بالایی هستند که به این معنی است که احتمال بیشتری وجود دارد که در نزدیکی یکدیگر قرار بگیرند. ارزش کم بین درخت سبز و آتش وحشی به این معنی است که این دو معمولاً دور از یکدیگر قرار دارند. شاخص مشارکت یک کران بالای تابع cross-K است. به دلیل ویژگی‌های محاسباتی‌اش، معیاری محبوب برای هم‌سازی است (Huang, Shekhar, and Xiong 2004). این شاخص از نسبت مشارکت استفاده می‌کند که معیار دیگری برای تشخیص هم‌سویی است. سهمیه مشارکت ویژگی f_1 در یک الگوی همنشینی CP، pr(CP، f_1) ، بخشی از ویژگی است f_1 که در الگو درگیر می شود . شاخص مشارکت به صورت تعریف شده است $pi(CP) = min_{f_i \in CP}pr(CP, f_i)$ . به عبارت دیگر، این حداقل نسبت مشارکت همه ویژگی های درگیر در الگوی collocation است. جدول 2b مقادیر شاخص مشارکت را برای الگوی همسویی در شکل 3a نشان می دهد. یکی از الگوها به $(\bigcirc، \مثلث)$ این معنی $pr((\bigcirc، \مثلث)، \bigcirc)$ است که 1 است زیرا همه دایره ها در الگوی collocation شرکت می کنند $(\bigcirc، \مثلث)$ . همچنین، دو مثلث درگیر الگوی collocation هستند $(\bigcirc، \مثلث)$ که به معنی $pr((\bigcirc، \مثلث)، \مثلث)$ = $\frac{2}{3} \تقریباً 0.67$ . بنابراین، $pi(\bigcirc، \مثلث) = 0.67$ که حداقل مقدار نسبت مشارکت ویژگی های درگیر در الگوی همنشینی است.

3.3 پیش بینی فضایی

پیش بینی فضایی، همچنین به عنوان طبقه بندی فضایی و رگرسیون شناخته می شود، برای شناسایی رابطه بین متغیرها در مجموعه داده های مختلف استفاده می شود. این متغیرها دو نوع هستند: متغیرهای توضیحی (یعنی ویژگی ها یا ویژگی های توضیحی) و متغیر هدف (همچنین به عنوان متغیر وابسته شناخته می شود). اگر متغیر هدف گسسته باشد، مشکل به عنوان طبقه بندی فضایی شناخته می شود. با این حال، زمانی که متغیرهای هدف پیوسته هستند، مشکل به عنوان رگرسیون فضایی نامیده می شود. پیش‌بینی فضایی هدف، پیش‌بینی ارزش متغیرهای هدف از روی متغیرهای توضیحی با استفاده از نمونه‌های آموزشی داده‌ها و روابط همسایگی بین مکان‌ها است.

داده‌کاوی سنتی و تکنیک‌های یادگیری ماشین به خوبی به پیش‌بینی فضایی تعمیم نمی‌یابند و اغلب عملکرد ضعیفی دارند (جیانگ و همکاران 2015). به عنوان مثال، در شکل 7b، یک درخت تصمیم برای طبقه بندی زمین های تالاب و خشک با استفاده از ویژگی های طیفی از یک تصویر ماهواره ای نشان داده شده در شکل 7a استفاده شده است. در مقایسه با حقیقت زمین در شکل 7c، خروجی درخت تصمیم حاوی مقدار زیادی خطای نمک و فلفل است. پیش‌بینی فضایی به روش‌هایی نیاز دارد که بتواند همبستگی و ناهمگنی فضایی را مدیریت کند (آلستاد و گتیس 2006؛ جیانگ و همکاران 2015).

مشکل طبقه بندی فضایی

شکل 7a-7c. مثالی از مسئله طبقه بندی فضایی چپ/الف: ورودی تصاویر هوایی با وضوح بالا. مرکز/ب: پیش‌بینی درخت تصمیم با خطاهای نمک و فلفل که در دایره سفید برجسته شده‌اند. راست/ج: نقشه حقیقت زمین: قرمز خشکی است، سبز تالاب است. منبع: نویسندگان

مدل خودرگرسیون فضایی (SAR) یک تکنیک یادگیری نظارت شده است که متعلق به خانواده مدل‌های رگرسیون فضایی است. از رابطه فضایی بین ویژگی های توضیحی برای پیش بینی متغیرهای هدف استفاده می کند. یک رابطه همسایگی برای مدل‌سازی رابطه فضایی ویژگی‌های توضیحی ضروری است و معمولاً یک ورودی اضافی برای SAR است. مدل SAR به صورت زیر تعریف می شود:

$y = \rho Wy + X\beta + \epsilon$ (2)

جایی دبلیو که یک ماتریس مجاورت است و وای اثر همسایگی را علاوه بر اثرات ویژگی های انتخاب شده ایکس و متغیر هدف مدل می کند. پارامترها $\rho$ را $\بتا$ می توان با استفاده از معادله 2 یاد گرفت. توجه کنید که رگرسیون خطی، که از فرض iid پیروی می کند، یک مورد خاص از مدل SAR است که $\rho$ صفر است. بنابراین، مدل SAR در مقایسه با مدل رگرسیون خطی کلی‌تر است.

برای مدل‌سازی ناهمگونی فضایی، می‌توانیم از یک تکنیک ناپارامتریک به نام رگرسیون وزن‌دار جغرافیایی (GWR) استفاده کنیم. GWR روی همه نمونه های داده رگرسیون انجام نمی دهد. درعوض، بر پیکربندی اندازه هسته تکیه می‌کند که در آن میانگین وزنی محلی را با استفاده از نمونه‌های همسایگی که در همان پهنای باند (به عنوان مثال، پنجره جستجو) با مکان داده فعلی (نقطه کانونی) هستند، محاسبه می‌کند. نمونه هایی که به مکان فعلی در پنجره جستجو نزدیکتر هستند وزن بیشتری خواهند داشت.

برای پرداختن به همبستگی خودکار فضایی در تصاویر هوایی، می‌توانیم از شبکه‌های عصبی کانولوشن (CNN) استفاده کنیم که با استفاده از داده‌های همسایگی، کانولوشن را انجام می‌دهند (سکوتی و همکاران 2020). با این حال، آنها ممکن است به تنوع فضایی نپردازند. بنابراین، شبکه‌های عصبی آگاه از تغییرپذیری فضایی (SVANN) پیشنهاد شده‌اند که فاصله را در حین آموزش شبکه‌های عصبی در نظر می‌گیرند (گوپتا، زی، و شکار 2020). در SVANN هر پارامتر یک نقشه است، یعنی تابعی از یک مکان. SVANN دو گزینه برای پیش بینی دارد. پیش‌بینی مبتنی بر منطقه از شبکه‌های عصبی محلی برای منطقه در دست برای پیش‌بینی استفاده می‌کند. رویکرد دوم ترکیب پیش‌بینی‌ها از تمام شبکه‌های عصبی محلی و ترجیح مدل‌های نزدیک با استفاده از وزن‌دهی فاصله است.

3.4 تشخیص نقاط پرت فضایی

نقاط پرت ممکن است جهانی یا مکانی باشند. نقاط دورافتاده جهانی نمونه‌های داده‌ای هستند که با بقیه نمونه‌های داده، مانند کلاهبرداری از کارت اعتباری، همخوانی ندارند. در مقابل، نقاط پرت فضایی تنها در همسایگی خود با سایر داده ها متفاوت است (شخار و همکاران 2011). به عنوان مثال، یک خانه جدید که توسط خانه های قدیمی در یک شهر توسعه یافته احاطه شده است را می توان یک نقطه پرت فضایی در نظر گرفت، اما ممکن است بر اساس سن کلی خانه های شهر، یک خانه پرت جهانی نباشد. در مثالی دیگر، شکل 8 نتایج انتخابات ریاست جمهوری ایالات متحده در سال 1992 را برای تمامی 50 ایالت نشان می دهد. ایندیانا نقطه پرت فضایی در این مثال است. تشخیص نقاط پرت فضایی برای برنامه هایی که نیاز به یافتن یک فعالیت یا اشیاء غیرمعمول یا مشکوک در مقایسه با همسایگی خود دارند، حیاتی است.

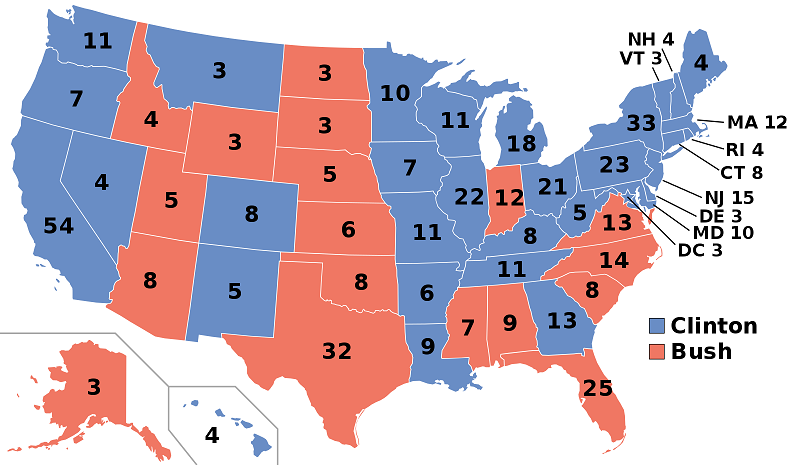
نتایج انتخابات 1992 نتایج ریاست جمهوری در سطح ایالت

شکل 8. نتایج انتخابات ریاست جمهوری ایالات متحده در سطح ایالتی از سال 1992. ایندیانا یک نقطه پرت فضایی است. منبع: نویسندگان

دو دسته از آزمون های آماری برای تشخیص نقاط پرت فضایی، آزمون های گرافیکی و آزمون های کمی وجود دارد. تست های گرافیکی از طریق تجزیه و تحلیل الگوهای تجسم شده از داده ها، نقاط پرت را تشخیص می دهند. به عنوان مثال می توان به ابرهای Variogram و نمودارهای پراکنده موران اشاره کرد. آزمون های کمی تفاوت بین ویژگی های غیر فضایی نقاط بازرسی شده و همسایگان فضایی آنها را محاسبه می کنند. هنگامی که تفاوت بزرگتر از یک آستانه از پیش تعریف شده باشد، یک نقطه پرت تشخیص داده می شود. آمار فضایی محله و نمودارهای پراکندگی آزمون های کمی هستند.

4. بحث و جهت گیری های آینده

همانطور که در شکل 9 نشان داده شده است، آمار مکانی و داده کاوی مکانی همپوشانی دارند. تکنیک های آماری فضایی (به عنوان مثال، آمار اسکن فضایی و تابع K ریپلی) از نظر ریاضی دقیق هستند که می توانند الگوهای شانس را حذف کنند و استحکام یک خروجی را از الگوریتم کاوی الگوی فضایی ارزیابی کنند. با این حال، یک چالش کلیدی در چنین تکنیک‌هایی مقیاس‌پذیری محاسباتی هنگام استفاده از داده‌های بزرگ فضایی است که حاوی هزاران ویژگی نقطه‌ای است که به‌طور تصاعدی رشد می‌کنند. این محدودیت‌های آمار فضایی را که به طور بالقوه در داده‌کاوی مکانی (SDM) مورد توجه قرار می‌گیرد، برجسته می‌کند. به عنوان مثال، در تشخیص هم‌سویی، شاخص مشارکت (هوانگ، شکر و شیونگ 2004) معرفی می‌شود که کران بالایی را روی تابع متقاطع K تعریف می‌کند، به طوری که با افزایش اندازه الگوی هم‌آهنگی، شاخص به‌طور یکنواخت کاهش می‌یابد (Xie et al. 2017).

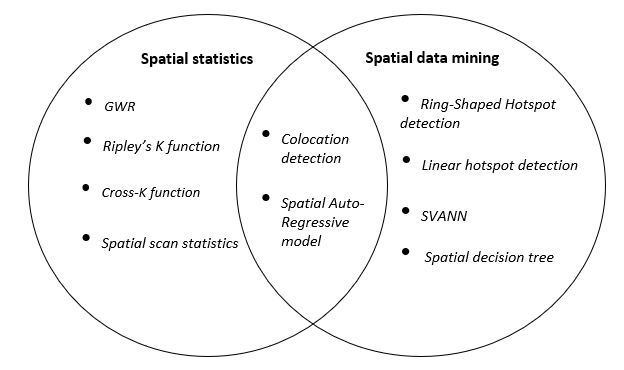
شکل 9. یک نمودار ون گویا برای برجسته کردن آمار فضایی و مفاهیم داده کاوی مکانی شرح داده شده در این مقاله. منبع: نویسندگان

اکثر تحقیقات در داده کاوی مکانی 1) فرض می کنند که فضا اقلیدسی و ایزومتریک است (یعنی ویژگی های آماری یکسانی در جهات مختلف دارد)، و 2) محله ها متقارن هستند. با این حال، در بسیاری از برنامه ها، فضا یک فضای شبکه است. برای مثال، شبکه‌های جاده‌ای و شبکه‌های رودخانه‌ای را می‌توان با استفاده از فضای شبکه به طور مؤثرتری مدل‌سازی کرد. توجه به ساختار شبکه یکی از چالش های استفاده از فضای شبکه است، اما تحقیقات در این زمینه نوید ارائه بینش دقیق تری را می دهد.

علاوه بر بعد فضا، بعد زمانی یکی دیگر از جنبه های مهم داده های مکانی است. اطلاعات و الگوهای مفید اغلب با افزودن یک بعد زمانی به تکنیک های SDM قابل شناسایی هستند. تشخیص نقطه زمانی که بر برخی پدیده ها تأثیر می گذارد یک مشکل کلیدی است که به آن تشخیص تغییر می گویند. به عنوان مثال، تشخیص تغییر کمک می کند تا زمانی که تغییرات آب و هوایی در یک منطقه رخ داده است، به طوری که می توان اقدامات حفاظتی مناسب را در آن منطقه انجام داد. در یک مشکل کشف اتصال از راه دور، مجموعه‌ای از سری‌های زمانی مکانی مکان‌های مختلف داریم. هدف کشف ارتباط از راه دور، یافتن جفت نقاط همبستگی مثبت یا منفی سری های زمانی در فواصل دور است. کشف ارتباط از راه دور در علم آب و هوا برای پیش‌بینی دقیق‌تر دمای مکان‌های مختلف جهان استفاده می‌شود.

در نهایت، کارشناسان حوزه منبع غنی از اطلاعات را برای بهبود مدل‌های فضایی مبتنی بر داده ارائه می‌کنند. مدل‌های شبیه‌سازی معمولاً قوانین فیزیکی و دانش حوزه مرتبط را در مدل‌های داده کاوی ادغام می‌کنند تا بینش‌های جدید و مفیدی به دست آورند (Karpatne et al. 2017). مدل‌های شبیه‌سازی معمولاً از منظر محاسباتی پیچیده هستند. در نتیجه، رویکردهای جدید علم داده مورد نیاز است که راه‌حل‌های تقریبی سریع مدل‌های شبیه‌سازی را پیاده‌سازی کند. با توجه به هزینه بالقوه بالای الگوهای جعلی در کاربردهای اجتماعی (به عنوان مثال، تجزیه و تحلیل الگوی جرم، شیوع بیماری)، مهم است که تکنیک های جدید از نظر آماری قوی باشند.

منابع:

Aldstadt, J. and Getis, A. (2006). استفاده از AMOEBA برای ایجاد ماتریس وزن های فضایی و شناسایی خوشه های فضایی. تحلیل جغرافیایی 38 (4): 327–343.

Cecotti, H., Rivera, A, Farhadloo, M., and Villarreal, M. (2020). تشخیص انگور با شبکه های عصبی کانولوشنال سیستم های خبره با برنامه های کاربردی 159 (113588). DOI: 10.1016/j.eswa.2020.113588 .

کرسی، ن. (2015). آمار برای داده های مکانی جان وایلی و پسران

Gelfand، AE، Diggle، P.، Guttrop، P.، و Fuentes، M. (2010). کتاب راهنمای آمار فضایی . مطبوعات CRC.

گوپتا، جی.، زی، ی.، و شکر، اس. (2020). “به سوی شبکه های عصبی عمیق آگاه از تغییرپذیری فضایی (SVANN): خلاصه ای از نتایج”. در: DeepSpatial2020، اولین کارگاه آموزشی ACM SIGKDD در مورد یادگیری عمیق برای داده ها، برنامه ها و سیستم های مکانی-زمانی.

هان، جی و میلر، اچ جی (2009). داده کاوی جغرافیایی و کشف دانش . مطبوعات CRC.

Huang, Y., Shekhar, S. and Xiong, H. (2004). کشف الگوهای مکان یابی از مجموعه داده های مکانی: یک رویکرد کلی IEEE Transactions on Knowledge and Data Engineering 16(12):1472-1485.

جیانگ، زی، شکر، اس.، ژو، ایکس، نایت، جی، و کورکوران، جی. (2015). یادگیری درخت تصمیم گیری فضایی مبتنی بر آزمون کانونی. IEEE Transactions on Knowledge and Data Engineering 27(6):1547-1559.

Karpatne, A., Alturi, G., Faghmous, JH, Steinbach, M., Banerjee, A., Ganguly, A., Shekhar, S., Samatova, N., and Kumar, V. (2017). علم داده مبتنی بر نظریه: پارادایم جدیدی برای کشف علمی از داده ها IEEE Transactions on Knowledge and Data Engineering 29(10): 2318-2331.

Kulldorff, M. (nd) SaTScanTM راهنمای کاربر، www. satscan org .

موهان، پی، شکر، اس.، شاین، جی، و راجرز، جی پی (2012). کشف الگوی مکانی-زمانی آبشاری. IEEE Transactions on Knowledge and Data Engineering 24(11):1977-1992.

Shekhar, S., Feiner, SK, and Aref, WG (2015a). محاسبات فضایی ارتباطات ACM 59 (1): 72-81.

Shekhar, S., Evans, MR, Kang, JM, and Mohan, P. (2011). شناسایی الگوها در اطلاعات مکانی: بررسی روش ها. بررسی های میان رشته ای وایلی: داده کاوی و کشف دانش 1 (3): 193-214.

Shekhar, S., Jiang, Z., Ali, R., Eftelioglu, E., Tang, X., Gunturi, VMV, an Zhou, X. (2015b). داده کاوی فضایی و زمانی: یک دیدگاه محاسباتی ISPRS International Journal of Geo-Information 4(4): 2306–2338.

Shekhar, S., and Vold, P. (2020). محاسبات فضایی سری MIT Press Essential Knowledge. کمبریج، MA: مطبوعات MIT.

Shekhar, S., Xiong, H., and Zhou, X. (Eds.) (2017). دایره المعارف GIS ، ویرایش دوم. انتشارات بین المللی Springer.

Tan, P.-N., Steinbach, M., and Kumar, V. (2006). مقدمه ای بر داده کاوی ، ویرایش اول. پیرسون.

Tang, X., Eftelioglu, E., Oliver, D., and Shekhar, S. (2017). کشف نقطه مهم خطی. معاملات IEEE روی داده های بزرگ 3(2): 140-153.

والر، لس آنجلس و گوتوی، کالیفرنیا (2004). آمار فضایی کاربردی برای داده های بهداشت عمومی. جان وایلی و پسران DOI: 10.1002/0471662682 .

Xie, Y., Eftelioglu, E., Ali, R., Tang, X., Li, Yl, Doshi, R., and Shekhar, S. (2017). مبانی فرا رشته ای علم داده های جغرافیایی. ISPRS International Journal of Geo-Information 6(12): 395. DOI: 10.3390/ijgi6120395

ژنگ، ی. (2015). داده کاوی مسیر: یک نمای کلی تراکنش های ACM روی سیستم ها و فناوری هوشمند (TIST). 6 (3): 1-41. DOI: 10.1145/2743025

اهداف یادگیری:

فرض iid را توضیح دهید و توضیح دهید که چرا برای داده های مکانی معتبر نیست
دو مفهوم کلیدی زیر را در آمار فضایی شرح دهید: خودهمبستگی مکانی و ناهمگنی فضایی.
MAUP را تعریف کنید و gerrymandering را به عنوان نمونه ای از MAUP توضیح دهید
سه حوزه آمار فضایی را فهرست کرده و به اختصار توضیح دهید
پنج الگوی فضایی را نام ببرید و آنها را به تصویر بکشید

سوالات ارزشیابی آموزشی:

کدام بیانیه(ها) فرض استقلال را نقض می کند؟
1. محمد لی» نامی نادر است، اگرچه «محمد» پرتکرارترین نام و «لی» بیشترین نام خانوادگی است.
2. چیزهای نزدیک بیشتر به هم مرتبط هستند تا چیزهای دور.
3. فریم‌های ویدیویی نزدیک اغلب افراد و اشیاء معمولی را نشان می‌دهند.
4. همه موارد فوق
کدام یک از سه تصویر در شکل 10 (زیر) بیشترین همبستگی مکانی را نشان می دهد؟
1. تصویر 10a
2. تصویر 10 ب
3. تصویر 10c
کدام گزاره(ها) فرض توزیع یکسانی را که در روش های آماری سنتی نهفته است، نقض می کند؟
1. ناهمگونی سلول های سرطانی درمان سرطان را دشوار می کند.
2. هیچ دو مکان روی زمین دقیقاً شبیه هم نیستند.
3. همه سیاست محلی است.
4. همه موارد فوق
کدام یک از موارد زیر ویژگی داده های مکانی است؟
1. خودهمبستگی
2. ناهمگونی
3. روابط ضمنی (مثلاً همسایه)
4. همه موارد فوق
کدام یک از موارد زیر به خود همبستگی فضایی نسبت داده نمی شود؟
1. شهرهای مجاور آب و هوای مشابهی دارند.
2. مناطق مجاور تمایل به کاشت محصولات کشاورزی مشابه دارند.
3. چیزهای نزدیک بیشتر به هم مرتبط هستند تا چیزهای دور.
4. نتایج داده‌کاوی مکانی در نزدیکی لبه‌های یک منطقه مورد مطالعه کمتر قابل اعتماد هستند.
کدام یک از موارد زیر در مورد جغرافیایی صحیح است:
1. این در مورد ترسیم مجدد مرزهای مناطق است.
2. می تواند به یک حزب یا گروه کمک کند تا از مزیت سیاسی استفاده کند.
3. می تواند نتیجه یک انتخابات را به گونه ای تغییر دهد که با رای مردم در تضاد باشد.
4. همه موارد فوق
خانواده‌های الگوی فضایی شامل نقاط داغ، هم‌مکان‌ها، پیش‌بینی‌های مکان و نقاط پرت فضایی هستند. هر سوال زیر با کدام الگو مطابقت دارد؟
1. کدام کشورها با همسایگان خود تفاوت زیادی دارند؟
2. کدام بخش‌های بزرگراه نرخ تصادفات غیرعادی بالایی دارند؟
3. طوفانی که بر فراز اقیانوس در حال دمیدن است به کجا خواهد رسید؟
4. کدام فروشگاه‌های خرده‌فروشی اغلب در مراکز خرید مشترک هستند؟
کدام یک خانواده الگوی نقطه کانونی فضایی را نشان نمی دهد؟
1. جاده هایی با نرخ غیرعادی بالای تصادفات رانندگی.
2. مناطقی با تمرکز غیرمعمول موزه ها.
3. شهرهایی با تعداد غیرمعمول زیادی دانش آموز در یک دوره آموزشی گسترده آنلاین خاص (MOOC) ثبت نام کردند.
4. محله ای با نرخ غیرعادی بالای یک بیماری عفونی (یا جرم).
کدام هم مکان را نشان نمی دهد؟
1. یک صدای بلند به طور موقت یک رعد و برق درخشان را دنبال می کند.
2. نیروگاه های هسته ای معمولاً در نزدیکی آب قرار دارند.
3. پرندگان سهره مصری در نزدیکی کروکودیل های نیل زندگی می کنند.
4. پردیس‌های کالج اغلب کتاب‌فروشی‌هایی در نزدیکی خود دارند.
کدام یک از موارد زیر در مورد نقاط پرت فضایی نادرست است؟
1. واحه (منطقه ایزوله از پوشش گیاهی) یک منطقه پرت فضایی در یک بیابان است.
2. پرت فضایی ممکن است ناپیوستگی و تغییرات ناگهانی را نشان دهد.
3. نقطه پرت فضایی به طور قابل توجهی با همسایگان فضایی آنها متفاوت است.
4. نقطه پرت فضایی به طور قابل توجهی با جمعیت به عنوان یک کل متفاوت است.

منابع اضافی:

مجموعه ای از 8 ویدیوی کوتاه در مورد داده کاوی مکانی که توسط Spatial Computing به اشتراک گذاشته شده است. مجموعه را می توان در اینجا به صورت آنلاین پیدا کرد .
شکر، س (2018). ویژگی داده کاوی مکانی چیست؟ ارائه. https://www-users.cs.umn.edu/~shekhar/talk/2018/sdm_5_9_2018_small.pdf
Shekhar, S., Xiong, H., and Zhou, X. (Eds.) (2017). دایره المعارف GIS ، ویرایش دوم. انتشارات بین المللی Springer.

وب جی آی اس (WebGIS)

Warning: ltrim() expects parameter 1 to be string, object given in /home/gisland1/public_html/wp-includes/formatting.php on line 4494

Warning: ltrim() expects parameter 1 to be string, object given in /home/gisland1/public_html/wp-includes/formatting.php on line 4494

داده کاوی مکانی – فضایی :کشف الگوهای پنهان در عوارض

مقدمه ای بر داده کاوی فضایی

قبلیطبقه بندی مکانی – فضایی :ناحیه بندی مهم و سرنوشت ساز برای سازمان ها

بعدیپایگاه داده مکانی فضایی :راه ها جدید کشف اطلاعات

مطالب مرتبط ...

GIS موبایل(بخش9)

شروع با ArcGIS API برای جاوا اسکریپت(قسمت8)

خدمات آنلاین تجزیه و تحلیل فضایی و پردازش جغرافیایی(قسمت7)

9 نظرات

دیدگاهتان را بنویسید لغو پاسخ