رایج ترین روش های نمونه برداری مکانی

رایج ترین روش های نمونه برداری مکانی

رایج ترین روش های نمونه برداری مکانی-موسسه چشم انداز-آموزش کاربردی GIS و RS

نمونه­ برداری تصادفی در مکان

يکي از روش ­هاي نمونه ­برداري روش تصادفي است. در اين روش همه اعضاي جمعيت شانس مساوي براي انتخاب شدن دارند و انتخاب يا عدم انتخاب عضوي در انتخاب عضو ديگر تأثیري ندارد. اين مسأله در مورد جمعيت ­هاي غير مکاني کاملاً قابل اجرا است برای نمونه در مورد مطالعه ويژگي هاي دانشجويان دانشگاه شیراز. اما در مورد پديده ­هاي مکانی مشکل دارد.

توبلر یکی از محققان برتر علوم جغرافیایی، وی قانون اول خود را در سال 1970 تدوین کرده است. مطابق با اين قانون هر عارضه ­ای بـه عارضه دیگـر وابســته اســت، امــا عوارض نزدیك تر بیشتر بـه هم وابسته ­اند، تـا عوارض دورتر (جنسن، 2009). به عبارت ديگر عوارضی که به هم نزدیک­ترند بیشترین تأثیر را نسبت به عوارض دورتر بر يکديگر دارند. بر طبق این اصل جغرافيايي:

اگر در يك واحد گونه گون روئيده است مطمئناً در واحد کناري هم گون روئيده است.

اکثر افراد یک منطقه از نظر سطح اقتصادی مشابه هم هستند و با دور شدن از آن منطقه ميزان شباهت ­ها کاهش مي­ يابد؛

ميانگين بارش ساليانه شهر مرودشت، که در فاصله 35 کيلومتري شمال شهر شيراز واقع شده، مشابهت زیادی با ميانگين بارش ساليانه شيراز دارد.

و …

همان طور که در مثال­ های فوق مشاهده می­ شود بین پدیده ­ها خود همبستگي مکاني وجود دارد. پديده­ هاي طبيعي معمولاً به صورت تجمعي وجود دارند. بنابراين اگر چه جغرافيدان ناگزير از استفاده از روش تصادفي است ولي بايد قبل از شروع عمليات اصلي، مطالعه علمي از منطقه داشته باشد و بداند که تغييرات مکاني ويژگي مورد مطالعه بر روي مکان چگونه است تا در نمونه­ برداري خود آن را در نظر بگيرد. فرآيند نمونه ­برداري تصادفي در واحدهاي نمونه پیوسته و ناپیوسته به صورت زیر انجام می ­شود:

رایج ترین روش های نمونه برداری مکانی

واحدهای نمونه ناپیوسته: فرآيند نمونه­ برداري تصادفي تقريباً آسان است. يعني اينکه به هرکدام از واحدها شماره داده مي­ شود و از روي جدول اعداد تصادفي، براساس شماره واحدها تعداد واحد مورد نياز انتخاب مي شود.

واحدهای نمونه پیوسته: در مورد داده ­هاي پيوسته بايستي منطقه مطالعه شبکه ­بندي شود به عبارتی دیگر فضاي يا قاب نمونه ­برداري را مي­ توان با شکل ­هاي مختلف قطعه ­بندي (شبکه ­بندي) کرده و سپس به طريق تصادفي از بين شبکه­ ها نمونه انتخاب می­ شود. در شکل زیر انواع شبکه­ بندي نشان داده شده است.

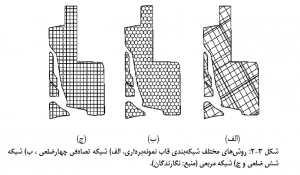
نحوۀ نمونه­ برداری در واحدهای پیوسته به اين صورت است که منطقه مطالعه در محور Xها و yها درجه­ بندي شده و شماره­ گذاري مي­ شود. براي تعيين هر واحد نقطه ­اي يا چهارگوش (مساحت) از جدول اعداد تصادفي يك عدد دو رقمي انتخاب مي­ شود که در آن عدد سمت چپ شماره محور Xها و رقم دست راست شماره محور yها باشد. محل تلاقي، واحد نقطه ­اي انتخاب شده مي­ باشد. براي چهارگوش ­ها اين دو رقم گوشه پايين و چپ آن را مشخص مي­کند و در مورد امتدادها اين دو رقم مکان يکي از دو سر امتداد مي تواند باشد. در شکل زیر روش­هاي مختلف نمونه­ برداري از شبکه نشان داده شده است.

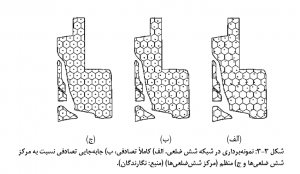
نمونه­ برداری سیستماتیک در مکان

در بسیاری از جامعه ­های طبیعی، شواهدی وجود دارند که در دنباله­ ای از واحدها که جامعه را می­ سازند و واحدها به صورتی مرتب قرار دارند، وقتی دو واحد با ترتیبهای i  و j مشاهده می­ شوند هر چه i و j به هم نزدیک تر باشند شباهت آن­ها بیشتر و هر چه از هم دورتر شوند شباهت آن­ها کمتر است. برای نمونه فرض کنید از ساحل دریای خزر تا تهران، به فاصله ­های 20 کیلومتر از هم ایستگاه ­های هواشناسی وجود داشته باشند و میزان باران هفتگی را اندازه گرفته. میزان بارندگی، رشته ­ای را تشکیل می­ دهد که به واحدهای آن همان شمارۀ ترتیب ایستگاه ­های هواشناسی از دریای خزر تا تهران را تخصیص دهیم. لذا رشته ­ای به صورت

تشکیل می­ شود. اگر yi و yj میزان بارندگی در نواحی اطراف ایستگاه شمارۀ i و شمارۀ  j باشند هر چه i و j نزدیک هم باشند این دو میزان بارندگی به هم نزدیک­ اند و هر چه دورتر باشند، میزان بارندگی در دو محل با هم بیشتر تفاوت دارند. به همین ترتیب فرض کنید نقطه ­ای مفروض بر قطعه زمینی قرار دارد که می ­خواهند در آن ساختمان­ بسازند و مقاومت خاک در آن نقطه را اندازه گرفته ­اند. اگر در طول خطی که از این نقطه می گذرد نقاطی به فاصلۀ 10 متر از هم در نظر گرفته شود هر چه نقطه­ ها از 0 دورتر باشند مقاومت خاک در آن­ها ممکن است تفاوتی بیشتر با مقاومت خاک در 0 داشته باشند. به خصوص مقاومت­ های خاک در دو نقطۀ نزدیک به هم مسلماً شبیه یکدیگرند. به طور کلی چنین وضعیتی وقتی وجود دارد که در پدیده ­ای طبیعی، نیروهای طبیعی کندی را، وقتی در طول دنباله پیش می­ رویم، موجب شود. جامعه­ هایی که دارای این ویژگی هستند به جامعه ­های خودهمبسته موسوم­ اند. مدل ریاضی برای بیان چنین حالتی این است که فرض شود yi و yj به طور مثبت همبسته بوده و همبستگی آن­ها تابعی از فاصلۀ جدایی انها، یعنی تابعی از i – j است، به قسمی که وقتی i – j زیاد می­ شود همبستگی کم می­ شود. این مدل ریاضـی می­ تواند نمایانگر برخی از صورت­ های برجسـتۀ جامعه­ های طبیعی محیط زندگی ما باشد. اگر برای زوجهای (yi, yj) با u = i – j، ضریب همبستگی را معین کرده این ضریب به u بستگی دارد. اگر ضریب همبستگی را با pu فرض شود با تغییر u تابع pu نموداری بر حسب u دارد که این نمودار را همبستگی نگار می­ نامند.

وقتی در جامعه ­های خود همبسته نمونه ­برداری با روش سیستماتیک، با روش طبقه ­بندی، و یا روش تصادفی ساده به دفعات بسیار زیاد صورت گیرد، در چنین جامعه ­هایی در درازمدت انجام نمونه­ برداری سیستماتیک در کل نتیجه­ ای بهتر از انجام روش­ های دیگر نمونه ­برداری دارد. به همین دلیل در اکثر جامعه ­های طبیعی، مثل جامعۀ یک مادۀ معدنی در یک ناحیه، جامعه قطر درختان یک جنگل، جامعه میزان ماه در یک ناحیه از دریا و … نظایر اینها از نمونه ­برداری سیستماتیک استفاده می­ کننند. پژوهشگران برای تابع pu در مورد پدیده ­هایی که زیاد مورد نیازند مدل­ هایی فراهم کرده ­اند. برای نمونه فیشر و مکنزی برای همبستگی بین مقدار بارندگی هفتگی دو ایستگاه هواشناسی که فاصلۀ جدایی آن­ها u است تابع

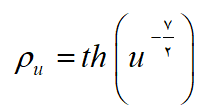
را به دست آورده ­اند. اسبرن و مترن در مورد همبستگی انبوهش جنگلها تابع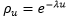

را فراهم کرده ­اند. و ولد برای بعضی از سری­ های زمانی در اقتصاد تابع

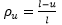
را پیشنهاد کرده است. این تبع­ ها از برازش تابع­ ها به مشاهدات نتیجه شده ­اند.

نمونه­ برداری طبقه بندی منظم و غیر مستقیم در مکان

اين روش که براي بار اول توسط بري (1962) پيشنهاد شد براي مطالعه کاربري زمين مناسب تشخيص داده شد. در اين روش منطقه مطالعه به واحدهاي مساوي و منظم برابر با اندازه نمونه مورد نياز تقسيم مي شود. در هر شبکه نقطه مورد نظر به صورت تصادفي انتخاب مي شود. به اين صورت که در رديف اول رقم  X به صورت تصادفي انتخاب شده براي همه سلول ها ثابت مي ­ماند و در هر سلول y به صورت تصادفي انتخاب مي شود (علیجانی، 1390).

روش­ هایی از نمونه­ برداری مکانی در دو بعد

در اينجا به برخی نمونه­ برداري فضايي دوبعدي پرداخته شده اما مفاهيم با نمونه­ برداري يک ­بعدي (برش عرضي) و سه­ بعدي (حجمي) مشابه می باشد.

در نمونه­ برداری تصادفی ساده از مشخصۀ نقاط یک ناحیۀ مسطح، معمولاً مربع مستطیل به ناحیۀ مزبور محیط می­ کنند و صفحۀ ناحیه را به محورهای مختصات مجهز می­ نمایند. سپس مطابق شکل 3-4 از اعداد حقیقی بین XA و XB عددی به تصادف به کمک جدول اعداد تصادفی استخراج می ­کنند بار دیگر از اعداد بین yA و yB نیز عددی به تصادف انتخاب می­ کنند. زوج تصادفی (X1,Y1) معرف نقطه ­ای در ناحیۀ S است که باید مشخصۀ آن را اندازه گرفت و اولین واحد نمونۀ تصادفی قرار داد. اعداد بین XA و XB و یا yA و yB را می­ توان اعداد صحیح یا اعداد دهدهی به فاصلۀ 1 و 0 از هم و یا برحسب نیاز، اعداد دهدهی دیگری در نظر گرفت. ممکن است نقطۀ (X1,y1) در ناحیۀ S و یا روی مرز آن قرار نگیرد، در این صورت از آن صرفنظر کرده عمل انتخاب تکرار می­ شود. تکرار انتخاب­ های نقاط ( Xi,Xy) با فرآیند مذکور آن قدر ادامه می ­یابد تا تعداد واحدهای مورد نظر برای نمونه انتخاب شوند. پس از انتخاب نقاط، همان طور که ذکر شد باید مشخصۀ مربوط ( برای نمونه مقاومت خاک در آن نقطه) را تعیین و نمونۀ تصادفی ساده دو بعدی را مشخص کرد.

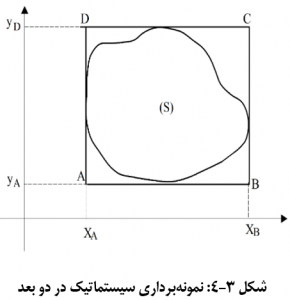
در مورد نمونه ­برداری سیستماتیک دو بعدی، روش کار تا حدی مشابه روش بالاست. ساده ­ترین الگو، گسترشی از نمونۀ سیستماتیک یک بعدی است که به الگوی ” شبکۀ مربعی” موسوم است. این الگوی شبکۀ مربعی به دو صورت هم تراز و ناهم تراز انجام می­ شود (عمیدی، 1383).

الگوی شبکه مربعی همتراز

در نمونه ­برداری سیستماتیک دو بعدی مطابق شکل زیر، ناحیۀ تحت نمونه ­برداری را مربعی فرض کرده که

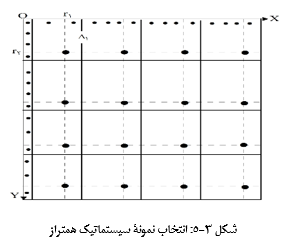
نقطۀ متساوی الفاصله به عنوان نقاط جامعه در سطح آن پراکنده ­اند (در شکل 3-5، یک ردیف طولی و یک ردیف عرضی را برای N = 16 نشان داده شده است) با نقطه­ های ناحیه، مشخصه­ ای همراه است که هدف، نمونه ­برداری از مقادیر این مشخصه است. در واقع جامعه، متشکل از

مقدار است. حال به جای تعیین مشخصۀ جامعه در

نقطه بخواهید نمونه ­ای سیستماتیک به حجم

تهیه شود به قسمی که

باشد. در روش همتراز دو محور OXو Oy را مطابق شکل کشیده و سطح مربع را به صورت شبکه­ ای در آورده که هر ضلع آن را به K قسمت n تایی تقسیم می ­کند و در کل

مربع کوچکتر به وجود می ­آورد. ابتدا از جدول اعداد تصادفی دو عدد تصادفی از 1 تا K انتخاب کرده تا زوج تصادفی (r1,r2) به وجود آید. این زوج را مطابق شکل، مختصات نقطۀ A گرفته که در مربع کوچک بالایی گوشۀ چپ قرار دارد. این نقطه را اولین نقطۀ نمونه در نظر گرفته و مشخصۀ مربوط به آن نقطه را اندازه ­گیری کرده و اولین واحد نمونۀ سیستماتیک قرار داده. اینک از نقطۀ A دو خط به موازات دو ضلع مربع اصلی رسم کرده و این فرآیند را تا انتخاب یک نقطه در هر مربع کوچک شبکه ادامه داده. توجه دارید که نقطه ­های منتخب در همۀ مربع­ های کوچک وضع مکانی مشابهی دارند. مقدار مشخصۀ مورد نظر را در تمام این نقاط معین کرده تا واحدهای نمونۀ سیستماتیک دو بعدی مشخـص شود. ملاحـظه می­ کنید که کار انتخاب نـمونه دقیقاً تعمیم روش نمونه­ برداری سیستماتیک یک بعدی است. این روش انتخاب نمونه را روش هم تراز می­ نامند. تعداد واحدهای نمونه

است. ماترن در 1960 نشان داده است که وقتی همبستگی بین هر دو نقطه در ناحیۀ مورد نظر، تابعی یکنوا، نزولی با تقعر مثبت از d فاصله نقاط باشد برای همبستگی نگارهایی نظیر

شبکۀ مربعی همتراز بسیار خوب عمل می ­کند. هینز در 14 آزمایش کشاورزی به این نتیجه رسیده است که نمونه ­برداری با شبکۀ مربعی همتراز تقریباً همان دقت نمونه ­برداری تصادفی سادۀ دو بعدی را دارد. میلن نقطۀ A را در مرکز انتخاب کرده است و به این نتیجه رسیده است که شبکۀ مربعی مرکزی بهتر از نمونه ­برداری تصادفی سادۀ دو بعدی حتی کمتر بهتر از نمونه­ برداری تصادفی با طبقه­ بندی عمل می ­کند (در بخش بعدی با این نمونه ­برداری آشنا می­ شوید).

شبکۀ مربعی ناهم تراز

جامعه را با

نقطه در نظر گرفته و شبکۀ مربع­ های کوچک را مثل حالت قبل تشکیل داده. در روش ناهم تراز انتخاب

نقطه در

مربع کوچک به صورت زیر انجام می­ شود:

الف) از اعداد 1 تا K دو عدد به تصادف انتخاب کرده. این دو زوج (r1,r2) را تشکیل می ­دهند. مطابق شکل نقطه A1 به مختصات (r1,r2) در مربع کوچک بالا و گوشۀ چپ مشخص می ­شود. A1 را اولین نقطۀ نمونه در نظر گرفته می­ شود.

ب) از نقطۀ A1 به موازات Oy خطی رسم کرده و روی آن A1B را برابر با K جدا کرده. از B به موازات محور OX خطی رسم کرده. سپس به کمک جدول اعداد تصادفی عددی از 1 تا k به تصادف انتخاب کرده. این عدد را r3 نامیده. روی این خط افقی نقطۀ A2 را به طول r3 معین کرده. A2 را دومین نقطۀ نمونه در نظر گرفته. به همین ترتیب روی امتداد A1B نقاط B2، B1، … خطوطی به موازات محور OX رسم کرده و از جدول اعداد تصادفی برای هر مربع عددی از 1 تا k به تصادف انتخاب کرده و نظیر روشی که A2 را مشخص کرده نقاط A4، A3، … را به کمک اعداد تصادفی انتخاب شده معین کرده. A4،A3، … نقاط دیگر نمونه هستند. به این ترتیب در تمام مربع­ های کوچک ستون اول نقاط نمونه مشخص می­ شوند.

ج) از نقطۀ A1 به موازات OX خطی رسم کرده و نقاط C1،C، … را به فاصلۀ k از هم و با شروع از A1 مشخص کرده. از این نقاط به موازات Oy خطوطی رسم کرده، سپس به کمک جدول اعداد تصادفی اعدادی از 1 تا k به تصادف انتخاب کرده و در تمام مربع­ های باقیماندۀ سطر اول به کمک این اعداد، روی خطوطی که رسم کرده نقاط تصادفی D2،D1، … را مشخص کرده. نقاط D2،D1،… را نیز به عنوان نقاط نمونه انتخاب کرده. تا اینجا 2n – 1 نقطه از نمونه به کمک  2n عدد تصادفی به دست آمده ­اند. حال در مربع ­های سطر دوم دقیقاً نقاطی را با همان فاصلۀ افقی A2 و فاصله های قائم D2،D1، … مشخص کرده. تا در هر مربع نقطۀ نمونه مشخص شود. این عمل را در تمام سطرها تکرار کرده تا همۀ نقاط نمونه معین شوند. این روش نمونه­ برداری سیستماتیک را ناهم تراز می­ خوانند. کنوویل برای همبستگی نگارهای ساده نشان داده است که روش ناهم تراز بر روش همتراز برتری دارد.

روش مربع لاتین

اين روش توسعه­ اي جديد در فناوري­ هاي نمونه ­برداري است که براي شبيه ­سازي دقيق توزيع احتمال داده­ هاي محيطي از طريق نمونه ­برداري تعداد کمتر سعي و خطا در مقايسه با ساير روش ­ها ابداع شده است. نکته کليدي در نمونه ­برداري به روش مربع لاتين، دسته­ بندي توزيع احتمال داده ­هاي محيطي است. توزيع احتمال تجمعي داده­ هاي محيطي از مقياس 0 تا 1 به فاصل مساوي تقسيم ­بندي مي­ شود. سپس از هر فاصله يا دسته توزيع احتمال تجمعي يک نمونه گرفته مي­شود. در اين روش از مقاديري در هر فاصله يک نمونه گرفته مي­ شود و در نهايت توزيع احتمال ورودي شبيه ­سازي مي­ شود. روش مربع لاتين، پوشش کاملی از هر متغیر را ایجاد می­ کند (مینازنی و مکبراتنی، 2006). مربع لاتین یک آرایه مربعی (ماتریس مربعی) است که در هر سطر و هر ستون آن اعضای مجموعه A به طور کامل و بدون تکرار قرار داشته باشند. به عنوان مثال در احتمالات ماتریس “متغیر تصادفی دوگانه” (که حاصل جمع هر سطر و ستون آن یک است) یک مربع لاتین است.

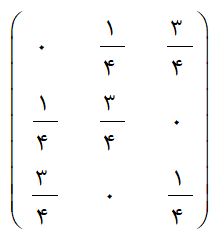
حال در مورد مستطیل ‌ها و مربع‌ هایی که درایه ‌های آن اعداد صحیح و مثبت هستند، یک مستطیل لاتین A با ابعاد P*q عبارت است از: یک ماتریس  که هر یک از درایه ‌های آن عضو مجموعه {n…1،2،3}بوده و هیچ عضو تکراری در سطر و یا ستون آن بوجود نیاید. در حالت خاص اگر P = q = n باشد يک مربع لاتین ايجاد مي­ شود. در این صورت هر سطر و هر ستون جایگشتی از مجموعه {n…1،2،3} است.

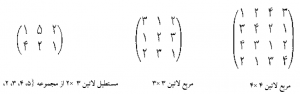
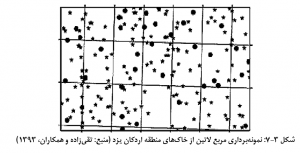
تقی ­زاده و همکاران (1393)، با استفاده از روش نمونه­ برداري مربع لاتين، به نقشه­ برداري رقومي کلاس خاک در منطقه اردکان يزد پرداخته­ اند (شکل 3-7).

روش فازی کی مینز

خوشه­ بندي، يکي از شاخه­ هاي يادگيري بدون نظارت است و فرايند خودکاري است که طي آن، نمونه­ ها به دسته­ هايي که اعضاي آن مشابه يکديگر هستند، تقسيم مي­ شوند و به اين دسته ­ها، خوشه گفته مي­ شود. الگوريتم کي­مينز يکي از روش­ هاي خوشه­ بندي ساده و سريع محسوب مي­ شود. اين الگوريتم با حرکت کردن بر روي مجموعه داده­ هاي محيطي قصد دارد تا اين داده­ها را به K خوشه دسته ­بندي کند. الگوريتم با انتخاب  عدد K داده انتخابي براي استفاده به عنوان خوشه اصلي به روش­ هاي مختلف (تصادفي و يا بر اساس اطلاعات اوليه در دسترس) شروع مي ­شود و مطالعه هر شاخه را محاسبه مي ­کند: در مرحله اول، با حرکت بر روي مجموعه داده­ ها و در نظر گرفتن ميانه خوشه ­ها، داده جديد به نزديک ­ترين خوشه اضافه مي­ شود. در مرحله دوم با اضافه شدن داده جديد براي هر خوشه، ميانه جديد محاسبه مي­ شود. اين کار تا زماني­ که تغييري در مرکز خوشه ايجاد نشود، ادامه مي­ يابد. در اين روش فاصله داخل خوشه­ ها کمينه  مي­ شود. تابع هدف به صورت معادله زير مي ­باشد (تقي­ زاده، 1394):

که در آن ∅ نماي فازي معادله است که درجه فازي شدن را نشان مي ­دهد و  ماتريس فاصله مي­ باشد و به صورت معادله زير محاسبه مي­ شود:

که در اين معادله A ماتريس نرمال شده فاصله است. کمينه ­سازي تابع هدف J راه ­حلي را براي ماتريس توابع عضويت M و مرکز خوشه C به صورت معادلات زير فراهم مي­ کند:

نماي فازي به زيرساخت ­هاي موجود در مجموعه داده­ ها و در نتيجه به تعداد مطلوب کلاس ­ها بستگي دارد. در واقع نماي فازي ميزان همپوشي کلاس­ ها را تعيين مي ­کند. بنابراين توابع اعتبارسنجي خوشه ­بندي، تا حدودي معياري براي سنجش فازي بودن نيز هستند؛ با اين وجود با بسط توابع عضويت فازي بايد مقدار مناسبي از ∅ را انتخاب کرد تا نماي فازي، زيرساخت­ هاي مجموعه داده­ ها را نشان دهد.

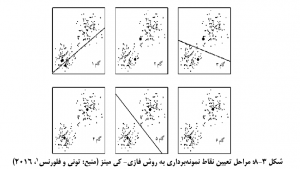
در شکل 3-8 روش مزبور به صورت ساده ­تر توضيح داده شده است. همان­گونه که ملاحظه مي­ شود در هر مرحله مرکز ثقل یا همان هسته مرکزی جابه جا می ­شود و به سمت مرکز خوشه­ ها حرکت می ­کند تا به بهترین نقطه یعنی میانگین خوشه ­ها برسد، در روش فازي کي مينز، تعداد خوشه ­ها از ابتدا مشخص و ثابت است اما در طول اجرا، تعلق داده ­ها  به خوشه تغییر می ­کند، هر داده (دایره­ای کوچک) به مرکز خوشه ­ای (دایره­ های بزرگتر) که به آن نزدیک تر است تعلق می ­گیرد.

روش چاردرخت

الگوريتم واريانس چاردرخت روشي سلسله مراتبي براي تقسيم­ کردن منطقه مورد مطالعه به واحدهاي همگن مي باشد. در اين روش ابتدا منطقه مورد مطالعه به چهار قسمت مساوي تقسيم مي­شود. در مرحله بعد، دوباره هر يک از نواحي ايجاد شده در مرحله قبل به چهار قسمت مساوي ديگر تقسيم مي­ شوند. لازم به ذکر مي ­باشد که از مرحله دوم به بعد، تقسيم ­بندي چهارتايي فقط در قسمت­ هايي از منطقه مورد مطالعه انجام مي­گيرد که داده­ هاي محيطي در آن جا داراي بيشترين واريانس باشند. الگوريتم اين فرآيند را آن ­قدر ادامه مي­ دهد تا واريانس در سلول­ هاي ايجاد شده حداقل شود؛ البته مي­ توان شرط اتمام الگوريتم چاردرخت را تکرار معيني نيز قرار داد. الگوريتم چاردرخت‌ها را می‌توان بر اساس نوع داده‌ای که نمایش می‌دهند (مثل سطح، نقطه، خط یا منحنی) تقسیم‌بندی کرد. یک نحوۀ دیگر تقسیم‌بندی بر این اساس است که آیا شکل درخت ایجاد شده مستقل از ترتیب پردازش داده­ ها است یا خیر. تعدادی از چاردرخت‌های متداول عبارتند از (دي برگ و همکاران، 2000):

الف) چاردرخت ناحیه‌ای

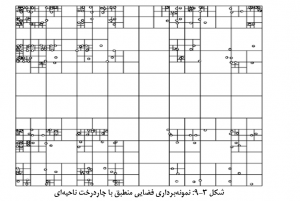
این نوع چاردرخت، نمایشگر افرازی از یک صفحۀ دو بعدی است که در آن افراز، صفحۀ دوبعدی به چهار ناحیۀ برابر افراز شده و برخی ناحیه ‌ها خود به چهار زیرناحیۀ برابر افراز شده‌اند و به همین ترتیب فرایند افراز می‌تواند ادامه پیدا کند. در چنین افرازی، هر گره، یا چهار فرزند دارد و یا فرزندی ندارد (برگ است). هر برگ از درخت مربوط به یکی از زیرناحیه‌ های افراز است و اطلاعات آن زیر ناحیه در آن برگ ذخیره می‌شود. چاردرخت ناحیه‌ای یک نوع ترای است. می‌توان از یک چاردرخت ناحیه‌ای با ارتفاع  برای نمایش یک تصویر با ابعاد 2 n*2n پیکسل (که مقدار هر پیکسل ۰ یا ۱ است) استفاده کرد. ریشۀ درخت، نمایشگر کل تصویر است. هر ناحیه‌ای که مقدار همۀ پیکسل‌هایش با هم برابر نیست، به ۴ زیرناحیه تقسیم می‌شود. در نهایت هر برگ از درخت، مجموعه ‌ای مربع ‌شکل از تعدادی پیکسل را نشان می‌دهد که همگی ۰ یا همگی ۱ هستند. اگر چاردرخت ناحیه‌ای برای نمایش مجموعه‌ای از نقاط (مثلاً تعدادی شهر که با طول و عرض جغرافیایی مشخص شده‌ اند) استفاده شود، ناحیه‌ها تا جایی تقسیم می ‌شوند که هر زیرناحیه حداکثر یک نقطه را شامل شود (شکل 3-9).

گره‌های درخت، خود نقاطی هستند که می‌خواهیم نمایش دهیم (برخلاف چاردرخت ناحیه‌ای، وقتی که برای نمایش تعدادی نقطه مورد استفاده قرار بگیرد). شکل ناحیه‌ های ایجاد شده به ترتیب اضافه کردن نقاط بستگی دارد (درست مثل درخت دودویی جستجو).

ب) چاردرخت نقطه‌ای

معمولاً برای مقایسه بین مجموعه‌ای از نقاط در صفحۀ دوبعدی بسیار بهینه (معمولاً از (O(log n) عمل می‌کند. در یک چاردرخت نقطه‌ای، گره ‌ها مشابه گره ‌های درخت دودویی هستند. با این تفاوت که در این‌جا هر گره به جای دو اشاره‌گر «راست» و «چپ» درخت دودویی، چهار اشاره‌گر دارد (به ازای هر زیرناحیه یک اشاره‌گر). همچنین کلید عناصر ذخیره‌شده به دو قسمت تقسیم می‌شود (نشان دهنده طول و عرض نقاط). با این توضیحات، در هر گره از درخت این اطلاعات وجود دارد:

– چهار اشاره‌گر: به ترتیب چارک NW، چارک NE، چارک  SW و چارک SE؛

– نقطه: که شامل کلید و مقدار می‌شود.کلید: معمولاً با دو مختصه X و y نمایش داده می‌شود. مقدار، مثلاً یک نام.

ج) چاردرخت یالی

این چاردرخت برای ذخیرۀ خط و منحنی (به جای نقطه) استفاده می‌شود. یک منحنی با تقسیمات زیاد ناحیه‌ ها تقریب زده می‌شود. این کار ممکن است باعث شود که یک درخت بسیار نامتوازن ایجاد شود که با هدف کاراتر شدن دسترسی‌ها تناقض دارد.

د) چاردرخت نقشۀ چندضلعی

این چاردرخت نوعی چاردرخت است که برای ذخیرۀ مجموعه‌ ای از چندضلعی ‌ها استفاده می‌شود که ممکن است تبهگون باشند (یعنی یک ضلع مجزا یا یک رأس مجزا در میانشان باشد). سه ردۀ اصلی از اين چار درخت­ ها وجود دارد که به دليل نوع داده‌هایی که در گره‌های سیاه ذخیره می‌شود تفاوت دارند. چاردرخت PM3 می‌تواند تعدادی ضلع نامتقاطع و حداکثر یک نقطه را ذخیره کند. چاردرخت PM2 همانند PM3 است با این تفاوت که همه ضلع‌ها باید نقطۀ پایانی یکسان داشته باشند. چاردرخت PM1 نیز شبیه PM2 است. ولی گره­ های سیاه می‌توانند یک نقطه و ضلع‌ های متصل به آن و یا فقط تعدادی ضلع که در یک نقطه مشترک هستند را در خود ذخیره کنند، ولی نمی ­توان یک نقطه و تعدادی ضلع که در آن نقطه مشترک نیستند را در گره ذخیره کرد.